  
Texture Mapping as a Fundamental Drawing Primitive
Paul Haeberli and Mark Segal
June 1993

Abstract
Texture mapping has traditionally been used to add realism to
computer graphics images. In recent years, this
technique has moved from the domain of software rendering systems to
that of high performance graphics hardware.
But texture mapping hardware can be used for many more applications
than simply applying diffuse patterns to polygons.
We survey applications of texture mapping including simple texture
mapping, projective textures, and image warping. We then describe
texture mapping techniques for drawing anti-aliased lines, air-brushes,
and anti-aliased text. Next we show how texture mapping may be used
as a fundamental graphics primitive for volume rendering, environment
mapping, color interpolation, contouring, and many other applications.
CR Categories and Subject Descriptors:
[Computer Graphics]: Picture/Image Generation;
I.3.7 [Computer Graphics]: Three-Dimensional Graphics and
Realism - color, shading, shadowing, texture-mapping, line drawing, and anti-aliasing
Introduction
Texture mapping[Catmull 74],[Heckbert 86]
is a powerful technique for adding realism to a
computer-generated scene.
In its basic form,
texture mapping lays an image (the texture) onto an object in a scene.
More general forms of texture mapping generalize the image to other
information;
an "image" of altitudes,
for instance,
can be used to control shading across a surface to achieve such effects
as bump-mapping.
Because texture mapping is so useful,
it is being provided as a standard rendering technique
both in graphics software interfaces and in computer graphics
hardware[Hanrahan 90][Deering 88].
Texture mapping can therefore be used in a scene with only a modest
increase in the complexity of the program that generates that scene,
sometimes with little effect on scene generation time.
The wide availability and high-performance of texture mapping makes it
a desirable rendering technique for achieving a number of effects that
are normally obtained with special purpose drawing hardware.
After a brief review of the mechanics of texture mapping,
we describe a few of its standard applications.
We go on to describe some novel applications of texture mapping.
Texture Mapping
When mapping an image onto an object,
the color of the object at each pixel is modified by a corresponding
color from the image.
In general,
obtaining this color from the image conceptually requires
several steps [Heckbert 89].
The image is normally stored as a sampled array,
so a continuous image must first be reconstructed from the samples.
Next,
the image must be warped to match any distortion (caused, perhaps,
by perspective) in the projected object being displayed.
Then this warped image is filtered to remove high-frequency
components
that would lead to aliasing in the final step: resampling to obtain the
desired color to apply to the pixel being textured.
In practice,
the required filtering is approximated by one of several methods.
One of the most popular is mipmapping[Williams 83].
Other filtering techniques may also be used [Crow 84].
There are a number of generalizations to this basic texture mapping scheme.
The image to be mapped need not be two-dimensional;
the sampling and filtering techniques may be applied for both one-
and three-dimensional images [Peachey 85].
In the case of a three-dimensional image,
a two-dimensional slice must be selected to be
mapped onto an object's boundary,
since the result of rendering must be two-dimensional.
The image may not be stored as an array but may be procedurally
generated [Peachey 85][Perlin 85].
Finally,
the image may not represent color at all,
but may instead describe transparency or other surface
properties to be used in lighting
or shading calculations [Carey 85].
Previous Uses of Texture Mapping
In basic texture mapping,
an image is applied to a polygon (or some other surface facet) by
assigning texture coordinates to the polygon's vertices.
These coordinates index a texture image,
and are interpolated across the polygon to determine,
at each of the polygon's pixels,
a texture image value.
The result is that some portion of the texture image is mapped onto
the polygon when the polygon is viewed on the screen.
Typical two-dimensional images in this application are
images of bricks or a road surface (in this case the texture image is often
repeated across a polygon);
a three-dimensional image might represent a block of marble from which
objects could be "sculpted."
Projective Textures
A generalization of this technique projects a texture onto surfaces as if
the texture were a projected slide or movie [Segal 92].
In this case the texture coordinates at a vertex
are computed as the result of the projection rather than being assigned
fixed values.
This technique may be used to simulate spotlights
as well as the reprojection of a photograph of an object back onto that
object's geometry.
Projective textures are also useful for simulating shadows.
In this case,
an image is constructed that represents distances from a light
source to surface points nearest the light source.
This image can be computed by performing Z-buffering from the light's
point of view and then obtaining the resulting Z-buffer.
When the scene is viewed from the eyepoint,
the distance from the light source to each point on a surface is computed
and compared to the corresponding value stored in the texture image.
If the values are (nearly) equal, then the point is not in shadow;
otherwise, it is in shadow.
This technique should not use mipmapping, because filtering must
be applied after the shadow comparison is
performed [Reeves 87].
Image Warping
Image warping may be implemented with texture mapping by defining
a correspondence between a uniform polygonal mesh (representing the original
image) and a warped mesh
(representing the warped image) [Oka 87].
The warp may be affine (to generate rotations, translations, shearings,
and zooms) or higher-order.
The points of the warped mesh are assigned the corresponding texture
coordinates of the uniform mesh,
and the mesh is texture mapped with the original image.
This technique allows for easily-controlled interactive image warping.
The technique can also be used for panning across a large texture
image by using a mesh that indexes only a portion of the entire image.
Transparency Mapping
Texture mapping may be used to lay transparent or semi-transparent objects
over a scene by representing transparency values in the texture image as
well as color values.
This technique is useful for simulating clouds [Gardner 85] and trees
for example,
by drawing appropriately textured polygons over a background.
The effect is that the background shows through around the edges of the
clouds or branches of the trees.
Texture map filtering applied to the transparency and color values
automatically leads to soft boundaries between the clouds or trees
and the background.
Surface Trimming
Finally,
a similar technique may be used to cut holes out of polygons or perform
domain space trimming on curved surfaces [Burns 92].
An image of the domain space trim regions is generated.
As the surface is rendered, its domain space coordinates are used to
reference this image.
The value stored in the image determines whether the corresponding point
on the surface is trimmed or not.
Additional Texture Mapping Applications
Texture mapping may be used to render objects that are
usually rendered by other, specialized means.
Since it is becoming widely available,
texture mapping may be a good choice to implement these techniques even
when these graphics primitives can be drawn using special purpose
methods.
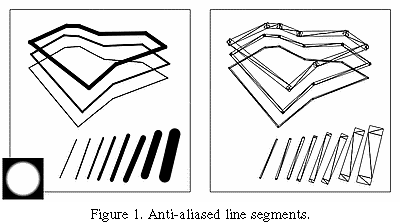
One simple use of texture mapping is to draw anti-aliased points of
any width.
In this case the texture image is of a filled circle with a smooth
(anti-aliased) boundary.
When a point is specified,
its coordinates indicate the center of a square whose width is determined
by the point size.
The texture coordinates at the square's corners are those corresponding
to the corners of the texture image.
This method has the advantage that any point shape may be accommodated
simply by varying the texture image.
A similar technique can be used to draw anti-aliased,
line segments of any width [Grossman 90].
The texture image is a filtered circle as used above.
Instead of a line segment,
a texture mapped rectangle, whose width is the desired line width,
is drawn centered on and aligned with the line segment.
If line segments with round ends are desired, these can be added
by drawing an additional textured rectangle on each end of the
line segment (Figure 1).
Air-brushes
Repeatedly drawing a translucent image on a background can
give the effect of spraying paint onto a canvas.
Drawing an image can be accomplished by drawing a texture mapped polygon.
Any conceivable brush "footprint", even a multi-colored one,
may be drawn using an appropriate texture image with
red, green, blue, and alpha. The brush image may also
easily be scaled and rotated (Figure 2).
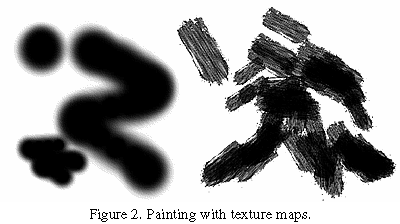
Anti-aliased Text
If the texture image is an image of a character,
then a polygon textured with that image will show that character
on its face.
If the texture image is partitioned into an array of rectangles,
each of which contains the image of a different character,
then any character may be displayed by drawing a polygon with appropriate
texture coordinates assigned to its vertices.
An advantage of this method is that strings of characters may be arbitrarily
positioned and oriented in three dimensions by appropriately positioning
and orienting the textured polygons.
Character kerning is accomplished simply by positioning the polygons
relative to one another (Figure 3).

Antialiased
characters of any size may be obtained with a single texture map simply
by drawing a polygon of the desired size,
but care must be taken if mipmapping is used.
Normally,
the smallest mipmap is 1 pixel square,
so if all the characters are stored in a single texture map,
the smaller mipmaps will contain a number of characters filtered together.
This will generate undesirable effects when displayed characters are too small.
Thus,
if a single texture image is used for all characters,
then each must be carefully placed in the image,
and mipmaps must stop at the point where the image of a single character
is reduced to 1 pixel on a side.
Alternatively,
each character could be placed in its own (small) texture map.
Volume Rendering
There are three ways in which texture mapping may be used to obtain
an image of a solid, translucent object.
The first is to draw slices of the object from back
to front [Drebin 88].
Each slice is drawn by first generating a texture image of the slice
by sampling the data representing the volume along the plane of the slice,
and then drawing a texture mapped polygon to produce the slice.
Each slice is blended with the previously drawn slices using transparency.
The second method uses 3D texture mapping [Drebin 92]. In this method,
the volumetric data is copied into the 3D texture image.
Then, slices perpendicular to the viewer are drawn.
Each slice is again a texture mapped polygon,
but this time the texture coordinates at the polygon's vertices
determine a slice through the 3D texture image.
This method requires a 3D texture mapping capability,
but has the advantage that texture memory need be loaded only once
no matter what the viewpoint.
If the data are too numerous to fit in a single 3D image, the
full volume may be rendered in multiple passes,
placing only a portion of the volume data into the texture image on each pass.
A third way is to use texture mapping to implement "splatting" as
described by [Westover 90][Laur 91].
Movie Display
Three-dimensional texture images may also be used to display
animated sequences [Akeley 93].
Each frame forms one two-dimensional slice of a three-dimensional
texture.
A frame is displayed by drawing a polygon with texture coordinates
that select the desired slice. This can be used to smoothly
interpolate between frames of the stored animation. Alpha values
may also be associated with each pixel to make animated "sprites".
Contouring
Contour curves drawn on an object can provide valuable information
about the object's geometry.
Such curves may represent height above some plane (as in a topographic
map) that is either fixed or moves with the object [Sabella 88].
Alternatively,
the curves may indicate intrinsic surface properties, such as geodesics
or loci of constant curvature.
Contouring is achieved with texture mapping by first defining a one-dimensional
texture image that is of constant color except at some spot along its length.
Then,
texture coordinates are computed for vertices of each polygon in the
object to be contoured using a texture coordinate generation function.
This function may calculate the distance of the vertex above some plane
(Figure 4),
or may depend on certain surface properties to produce,
for instance,
a curvature value.
Modular arithmetic is used in texture coordinate interpolation to effectively
cause the single linear texture image to repeat over and over.
The result is lines across the polygons that comprise an object, leading
to contour curves.

A two-dimensional (or even three-dimensional) texture image may be used
with two (or three) texture coordinate generation functions to produce
multiple curves,
each representing a different surface characteristic.
Generalized Projections
Texture mapping may be used to produce a non-standard projection of
a three-dimensional scene,
such as a cylindrical or spherical projection [Greene 86].
The technique is similar to image warping.
First,
the scene is rendered six times from a single viewpoint,
but with six distinct viewing directions: forward, backward, up, down,
left, and right.
These six views form a cube enclosing the viewpoint.
The desired projection is formed by projecting the cube of images
onto an array of polygons (Figure 5).

Color Interpolation in non-RGB Spaces
The texture image may not represent an image at all,
but may instead be thought of as a lookup table.
Intermediate values not represented in the table are obtained
through linear interpolation,
a feature normally provided to handle image filtering.
One way to use a three-dimensional lookup table is to fill it
with RGB values that correspond to, for instance,
HSV (Hue, Saturation, Value) values.
The H, S, and V values index the three dimensional tables.
By assigning HSV values to the vertices of a polygon
linear color interpolation may be carried out in HSV space
rather than RGB space.
Other color spaces are easily supported.
Phong Shading
Phong shading with an infinite light and a local viewer
may be simulated using a 3D texture image as follows.
First,
consider the function of x, y, and z that assigns a brightness
value to coordinates that represent a (not necessarily unit length)
vector.
The vector is the reflection off of the surface of the vector from the
eye to a point on the surface, and is thus a function of the normal
at that point.
The brightness function depends on the location of the light source.
The 3D texture image is a lookup table for the brightness
function given a reflection vector.
Then,
for each polygon in the scene,
the reflection vector is computed at each of the polygon's vertices.
The coordinates of this vector are interpolated across the polygon
and index the brightness function stored in the texture image.
The brightness value so obtained modulates the color of the polygon.
Multiple lights may be obtained by incorporating multiple brightness
functions into the texture image.
Environment Mapping
Environment mapping [Greene 86]
may be achieved through texture mapping in one of two ways.
The first way requires six texture images,
each corresponding to a face of a cube,
that represent the surrounding environment.
At each vertex of a polygon to be environment mapped,
a reflection vector from the eye off of the surface is computed.
This reflection vector indexes one of the six texture images.
As long as all the vertices of the polygon generate reflections into the
same image,
the image is mapped onto the polygon using projective texturing.
If a polygon has reflections into more than one face of the cube,
then the polygon is subdivided into pieces,
each of which generates reflections into only one face.
Because a reflection vector is not computed at each pixel,
this method is not exact,
but the results are quite convincing when the polygons are small.
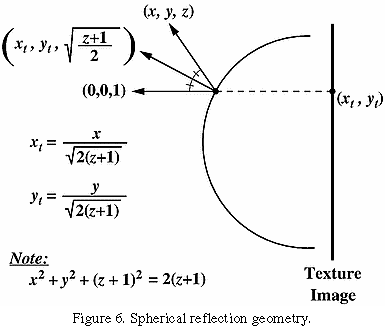
The second method is to generate a single texture image
of a perfectly reflecting sphere in the environment.
This image consists of a circle representing the hemisphere of the
environment behind the viewer,
surrounded by an annulus representing the hemisphere in front of the viewer.
The image is that of a perfectly reflecting
sphere located in the environment when the viewer is infinitely far from the
sphere.
At each polygon vertex,
a texture coordinate generation function generates coordinates that
index this texture image, and these are interpolated across the polygon.
If the (normalized) reflection vector at a vertex
is r = vect(x y z),
and m = sqrt(2*(z+1)),
then the generated coordinates are x/m and y/m
when the texture image is indexed by coordinates ranging from -1 to 1.
(The calculation is diagrammed in Figure 6.)
This method has the disadvantage that the texture image must be recomputed
whenever the view direction changes,
but requires only a single texture image with no special polygon subdivision
(Figure 7).

3D Halftoning
Normal halftoned images are created by thresholding a
source image with a halftone screen. Usually this
halftone pattern of lines or dots bears no direct
relationship to the geometry of the scene.
Texture mapping allows halftone patterns to be generated using a 3D spatial
function or parametric lines of a surface (Figure 8).
This permits us to
make halftone patterns that are attached to the surface
geometry [Saito 90].

Conclusion
Many graphics systems now provide hardware that supports
texture mapping. As a result, generating a texture mapped
scene need not take longer than generating a scene without
texture mapping.
We hope to have shown that,
in addition to its standard uses,
texture mapping can be used for a large number of interesting
applications, and that texture mapping is a powerful and
flexible low level graphics drawing primitive.
References
[Akeley 93] Kurt Akeley,
Personal Communication, 1993.
[Bishop 86] G. Bishop and D. M. Weimer,
Fast Phong Shading,
Computer Graphics (SIGGRAPH '86 Proceedings), Pages 103-106, August, 1986.
[Burns 92] Derrick Burns,
Personal Communication, 1992.
[Carey 85] Richard J. Carey and Donald P. Greenberg,
Textures for Realistic Image Synthesis,
Computer and Graphics, Pages 125-138, Vol. 9, No.3, 1985.
[Catmull 74] Ed Catmull,
A Subdivision Algorithm for Computer Display of Curved Surfaces,
PhD Thesis, University of Utah, 1974.
[Crow 84] Frank Crow,
Summed-Area Tables for Texture Mapping,
Computer Graphics (SIGGRAPH '84 Proceedings), Pages 207-212, July, 1984.
[Deering 88] Michael Deering and Stephanie Winner and Bic Schediwy and
Chris Duffy and Neil Hunt,
The Triangle Processor and Normal Vector Shader: A VLSI
System for High Performance Graphics,
Computer Graphics (SIGGRAPH '88 Proceedings), Pages 21-30, August, 1988.
[Drebin 88] Robert A. Drebin and Loren Carpenter and Pat Hanrahan,
Volume Rendering,
Computer Graphics (SIGGRAPH '88 Proceedings), Pages 65-74, August, 1988.
[Drebin 92] Robert A. Drebin,
Personal Communication, 1992.
[Gardner 85] Geoffrey. Y. Gardner,
Visual Simulation of Clouds,
Computer Graphics (SIGGRAPH '85 Proceedings), Pages 297-303, July, 1985.
[Greene 86] Ned Greene,
Applications of World Projections,
Proceedings of Graphics Interface '86, Pages 108-114, May, 1986.
[Grossman 90] Mark Grossman,
Personal Communication, 1990.
[Hanrahan 90] Pat Hanrahan and Jim Lawson,
A Language for Shading and Lighting Calculations,
Computer Graphics (SIGGRAPH '90 Proceedings), Pages 289-298, August, 1990.
[Heckbert 86] Paul S. Heckbert,
Survey of Texture Mapping,
IEEE Computer Graphics and Applications, Pages 56-67, November, 1986.
[Heckbert 89] Paul S. Heckbert,
Fundamentals of Texture Mapping and Image Warping,
M.Sc. Thesis, Department of Electrical Engineering and Computer Science,
University of California, Berkeley, June, 1989.
[Laur 91] David Laur and Pat Hanrahan,
Hierarchical splatting: A progressive refinement algorithm for volume rendering,
Computer Graphics (SIGGRAPH '91 Proceedings), Pages 285-288, July, 1991.
[Oka 87] Masaaki Oka and Kyoya Tsutsui and Akio Ohba and Yoshitaka,
Real-Time Manipulation of Texture-Mapped Surfaces,
Computer Graphics (SIGGRAPH '87 Proceedings), July, 1987.
[Peachy 85] Darwyn R. Peachey,
Solid Texturing of Complex Surfaces,
Computer Graphics (SIGGRAPH '85 Proceedings), Pages 279-286, July, 1985.
[Perlin 85] Ken. Perlin,
An Image Synthesizer,
Computer Graphics (SIGGRAPH '85 Proceedings), Pages 287-296, July, 1985.
[Reeves 87] William Reeves and David Salesin and Rob Cook,
Rendering Antialiased Shadows with Depth Maps,
Computer Graphics (SIGGRAPH '87 Proceedings), Pages 283-291, July, 1987.
[Sabella 88] Paolo Sabella,
A Rendering Algorithm for Visualizing 3D Scalar Fields,
Computer Graphics (SIGGRAPH '88 Proceedings), Pages 51-58, August, 1988.
[Saito 90] Takafumi Saito and Tokiichiro Takahashi,
Comprehensible Rendering of 3-D Shapes,
Computer Graphics (SIGGRAPH '90 Proceedings), Pages 197-206, August, 1990.
[Segal 92] Mark Segal and Carl Korobkin and Rolf van Widenfelt and Jim
Foran and Paul Haeberli,
Fast Shadows and Lighting Effects using Texture Mapping,
Computer Graphics (SIGGRAPH '92 Proceedings), Pages 249-252, July, 1992.
[Westover 90] Lee Westover,
Footprint Evaluation for Volume Rendering,
Computer Graphics (SIGGRAPH '90 Proceedings), Pages 367-376, August, 1990.
[Whitted 83] Turner Whitted,
Anti-Aliased Line Drawing Using Brush Extrusion,
Computer Graphics (SIGGRAPH '83 Proceedings), Pages 151-156, July, 1983.
[Williams 83] Lance Williams,
Pyramidal Parametrics,
Computer Graphics (SIGGRAPH '83 Proceedings), Pages 1-11, July, 1983.
This paper appeared in the proceedings of the Fourth Eurographics Workshop
on Rendering, Michael Cohen, Claude Puech, Francois Sillion, Editors.
Paris, France, June, 1993.

|